İki Küp Arasındaki Farkı Bulma ve Çarpanlara Ayırma Formülü ile İlgili Örnekler ve Yöntemler için Tam Küp Açılımı Kılavuzu
Küp Açılımı Formülleri ve Örnek Sorular
Matematik denilince akla hemen formüller gelir. Özellikle üniversiteye giriş sınavları, KPSS ve ALES gibi sınavlardaki sorularda bize kolaylık sağlayacak formüllere ihtiyaç duyarız.
Küp açılımı formülü, özellikle çarpanlara ayırmada kullanılır ve son derece önemlidir. Küp açılımı nasıl yapılır hep birlikte bakalım Küp açılımı nedir? Çarpanlara ayırmadaki önemi büyük olan küp açılımı, (x³ + y³) şeklinde ifade ettiğimiz açılımlara denir.
Sınavlarda en çok karşılaşılan soru formatları, iki ifadenin toplamı-farkının küpü ya da iki ifadenin küpünün toplamı-farkı şeklindedir. Bu açılımları formüle dökecek olursak;
- İki küp toplamı: x³ + y³ = (x + y).(x² – xy + y²)
- İki küp farkı: x³ – y³ = (x – y).(x² + xy + y²)
- İki ifadenin toplamının küpü: (x + y)³ = x³ + 3x² y + 3xy² + y³
- İki ifadenin farkının küpü: (x y)³ = x³ 3x² y + 3xy² y³
Yukarıda gösterdiğimiz formüller tam küp açılımı formülleri olup bu formülleri ezberledikten sonra sınavlarda rahatlıkla soruları çözebilirsiniz.
Çarpanlara ayırma küp açılımına örneklerle konuyu anlamak için şu sorulara bakalım:
ÖRNEK SORU 1: x³ 27 ifadesini çarpanlarına ayırınız: x3 33 = (x-3).(x² + 3x + 9)
ÖRNEK SORU 2: x³ + 125 ifadesini çarpanlarına ayırınız: x3 + 53 = (x+5).(x² 5x + 25)
ÖRNEK SORU 3: İki reel sayının toplamı 7 ve çarpımları 10 ise küplerinin toplamı nedir? İfademizi çözebilir ve sonuca ulaşabiliriz.
Formülleri öğrendikten sonra, sınavlarda karşılaşabileceğiniz küp açılımı sorularını evde pratik yaparak çözerek kendinizi geliştirebilirsiniz.
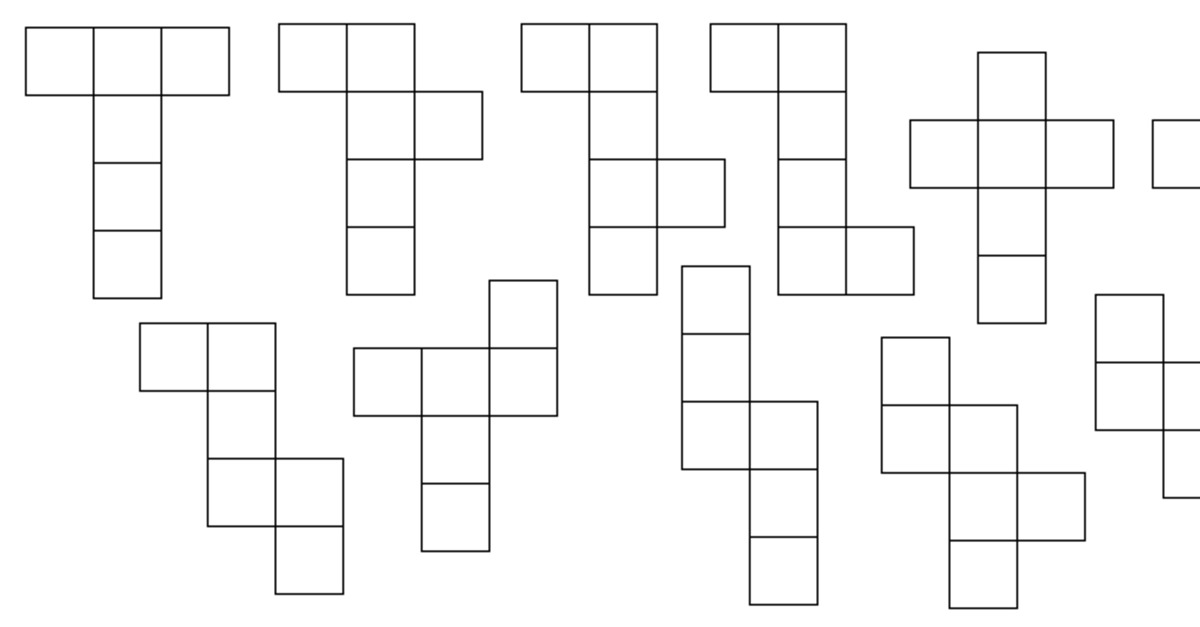
Küp nedir? Tüm yüzleri kare olan dikdörtgen prizmasına küp denir. Kenarları katlayarak farklı şekillerde 11 farklı küp prizma oluşturulabilir. Bu şekilleri inceleyerek küp kavramını daha iyi anlayabilirsiniz.

